Стремимся к нулю
Бесконечно-малые и бесконечно-большие функции. Сравнение бесконечно малых функций
Бесконечно малая — числовая функция или последовательность, которая стремится к нулю.
Бесконечно большая — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Сравнение бесконечно малых
Определения[править | править вики-текст]
Допустим, у нас есть бесконечно малые при одном и том же 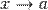 величины
величины 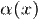 и
и 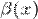 (либо, что не важно для определения, бесконечно малые последовательности).
(либо, что не важно для определения, бесконечно малые последовательности).
· Если 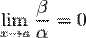 , то
, то 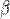 — бесконечно малая высшего порядка малости, чем
— бесконечно малая высшего порядка малости, чем 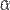 . Обозначают
. Обозначают 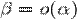 или β≺α.
или β≺α.
· Если 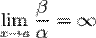 , то
, то 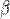 — бесконечно малая низшего порядка малости, чем
— бесконечно малая низшего порядка малости, чем 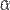 . Соответственно
. Соответственно 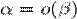 или α≺β.
или α≺β.
· Если 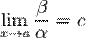 (предел конечен и не равен 0), то
(предел конечен и не равен 0), то 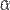 и
и 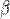 являются бесконечно малыми величинами одного порядка малости. Это обозначается какα≍β или как одновременное выполнение отношений
являются бесконечно малыми величинами одного порядка малости. Это обозначается какα≍β или как одновременное выполнение отношений 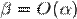 и
и 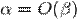 . Следует заметить, что в некоторых источниках можно встретить обозначение, когда одинаковость порядков записывают в виде только одного отношения «о большое», что является вольным использованием данного символа.
. Следует заметить, что в некоторых источниках можно встретить обозначение, когда одинаковость порядков записывают в виде только одного отношения «о большое», что является вольным использованием данного символа.
· Если 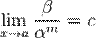 (предел конечен и не равен 0), то бесконечно малая величина
(предел конечен и не равен 0), то бесконечно малая величина 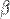 имеет
имеет 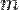 -й порядок малости относительно бесконечно малой
-й порядок малости относительно бесконечно малой 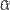 .
.
Для вычисления подобных пределов удобно использовать правило Лопиталя.
Примеры сравнения[править | править вики-текст]
· При 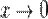 величина
величина 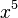 имеет высший порядок малости относительно
имеет высший порядок малости относительно 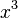 , так как
, так как 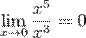 . С другой стороны,
. С другой стороны, 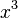 имеет низший порядок малости относительно
имеет низший порядок малости относительно 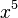 , так как
, так как 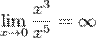 .
.
С использованием О-символики полученные результаты могут быть записаны в следующем виде 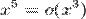 .
.
· 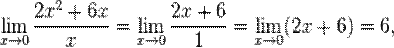 то есть при
то есть при 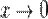 функции
функции 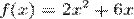 и
и 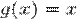 являются бесконечно малыми величинами одного порядка.
являются бесконечно малыми величинами одного порядка.
В данном случае справедливы записи 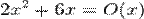 и
и 
· При 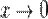 бесконечно малая величина
бесконечно малая величина 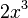 имеет третий порядок малости относительно
имеет третий порядок малости относительно 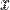 , поскольку
, поскольку 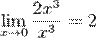 , бесконечно малая
, бесконечно малая 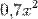 — второй порядок, бесконечно малая
— второй порядок, бесконечно малая 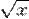 — порядок 0,5.
— порядок 0,5.
Бесконечно малая величина
Бесконечно малая величина
Бесконечно малая величина — числовая функция или последовательность, которая стремится к нулю.
Бесконечно большая величина — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Содержание
Исчисление бесконечно малых и больших
Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная сумма бесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений, составляющих основу современной высшей математики. Понятие бесконечно малой величины тесно связано с понятием предела.
Бесконечно малая
Последовательность an называется бесконечно малой, если 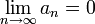 . Например, последовательность чисел
. Например, последовательность чисел 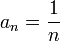 — бесконечно малая.
— бесконечно малая.
Функция называется бесконечно малой в окрестности точки x , если 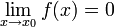 .
.
Функция называется бесконечно малой на бесконечности, если 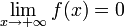 либо
либо 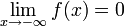 .
.
Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если 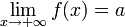 , то f(x) − a = α(x) ,
, то f(x) − a = α(x) , 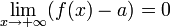 .
.
Бесконечно большая величина
Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsinx , неограниченная с обеих сторон, не является бесконечно большой при 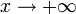 .
.
Последовательность an называется бесконечно большой, если 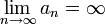 .
.
Функция называется бесконечно большой в окрестности точки x , если 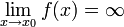 .
.
Функция называется бесконечно большой на бесконечности, если 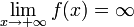 либо
либо 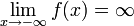 .
.
Свойства бесконечно малых и бесконечно больших
- Сумма конечного числа бесконечно малых — бесконечно малая.
- Произведение бесконечно малых — бесконечно малая.
- Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
- Если an — бесконечно малая последовательность, сохраняющая знак, то
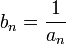 — бесконечно большая последовательность.
— бесконечно большая последовательность.
Сравнение бесконечно малых величин
Как сравнивать бесконечно малые величины?
Отношение бесконечно малых величин образует так называемую неопределённость  .
.
Определения
Допустим, у нас есть бесконечно малые при одном и том же 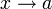 величины α(x) и β(x) (либо, что не суть важно для определения, бесконечно малые последовательности).
величины α(x) и β(x) (либо, что не суть важно для определения, бесконечно малые последовательности).
- Если
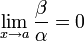 , то β — бесконечно малая высшего порядка малости, чем α . Обозначают β = o(α) .
, то β — бесконечно малая высшего порядка малости, чем α . Обозначают β = o(α) . - Если
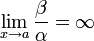 , то β — бесконечно малая низшего порядка малости, чем α . Соответственно α = o(β) .
, то β — бесконечно малая низшего порядка малости, чем α . Соответственно α = o(β) .
- Если
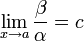 (предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.
(предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.
Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).
- Если
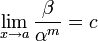 (предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α .
(предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α .
Для вычисления подобных пределов удобно использовать правило Лопиталя.
Примеры сравнения
- При
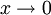 величина x 5 имеет высший порядок малости относительно x 3 , так как
величина x 5 имеет высший порядок малости относительно x 3 , так как 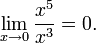 С другой стороны, x 3 имеет низший порядок малости относительно x 5 , так как
С другой стороны, x 3 имеет низший порядок малости относительно x 5 , так как 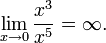
С использованием О-символики полученные результаты могут быть записаны в следующем виде x 5 = o(x 3 ).
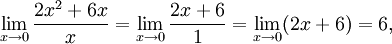 то есть при
то есть при 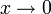 функции f(x) = 2x 2 + 6x и g(x) = x являются бесконечно малыми величинами одного порядка.
функции f(x) = 2x 2 + 6x и g(x) = x являются бесконечно малыми величинами одного порядка.
В данном случае справедливы записи 2x 2 + 6x = O(x) и x = O(2x 2 + 6x).
- При
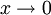 бесконечно малая величина 2x 3 имеет третий порядок малости относительно x , поскольку
бесконечно малая величина 2x 3 имеет третий порядок малости относительно x , поскольку 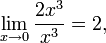 бесконечно малая 0,7x 2 — второй порядок, бесконечно малая
бесконечно малая 0,7x 2 — второй порядок, бесконечно малая 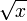 — порядок 0,5 .
— порядок 0,5 .
Эквивалентные величины
Определение
Если 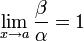 , то бесконечно малые величины α и β называются эквивалентными (
, то бесконечно малые величины α и β называются эквивалентными (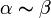 ).
).
Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.
При 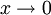 справедливы следующие соотношения эквивалентности (как следствия из т.н. замечательных пределов):
справедливы следующие соотношения эквивалентности (как следствия из т.н. замечательных пределов):
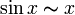 ;
;
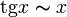 ;
;
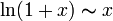 ;
;
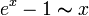 .
.
Данная теорема имеет прикладное значение при нахождении пределов (см. пример).
Пример использования
- Найти
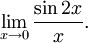
Заменяя sin2x эквивалентной величиной 2x , получаем 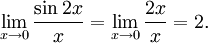
Исторический очерк
Понятие «бесконечно малое» обсуждалось ещё в античные времена в связи с концепцией неделимых атомов, однако в классическую математику не вошло. Вновь оно возродилось с появлением в XVI веке «метода неделимых» — разбиения исследуемой фигуры на бесконечно малые сечения.
В XVII веке произошла алгебраизация исчисления бесконечно малых. Они стали определяться как числовые величины, которые меньше всякой конечной (ненулевой) величины и всё же не равны нулю. Искусство анализа заключалось в составлении соотношения, содержащего бесконечно малые (дифференциалы), и затем — в его интегрировании.
Математики старой школы подвергли концепцию бесконечно малых резкой критике. Мишель Ролль писал, что новое исчисление есть «набор гениальных ошибок»; Вольтер ядовито заметил, что это исчисление представляет собой искусство вычислять и точно измерять вещи, существование которых не может быть доказано. Даже Гюйгенс признавался, что не понимает смысла дифференциалов высших порядков.
Споры в Парижской Академии наук по вопросам обоснования анализа приобрели настолько скандальный характер, что Академия однажды вообще запретила своим членам высказываться на эту тему (в основном это касалось Ролля и Вариньона). В 1706 году Ролль публично снял свои возражения, однако дискуссии продолжались.
В 1734 году известный английский философ, епископ Джордж Беркли выпустил нашумевший памфлет, известный под сокращенным названием «Аналист». Полное его название: «Аналист или рассуждение, обращенное к неверующему математику, где исследуется, более ли ясно воспринимаются или более ли очевидно выводятся предмет, принципы и умозаключения современного анализа, чем религиозные таинства и догматы веры».
«Аналист» содержал остроумную и во многом справедливую критику исчисления бесконечно малых. Метод анализа Беркли считал несогласным с логикой и писал, что, «как бы он ни был полезен, его можно рассматривать только как некую догадку; ловкую сноровку, искусство или скорее ухищрение, но не как метод научного доказательства». Цитируя фразу Ньютона о приращении текущих величин «в самом начале их зарождения или исчезновения», Беркли иронизирует: «это ни конечные величины, ни бесконечно малые, ни даже ничто. Не могли ли бы мы их назвать призраками почивших величин?… И как вообще можно говорить об отношении между вещами, не имеющими величины. Тот, кто может переварить вторую или третью флюксию [производную], вторую или третью разность, не должен, как мне кажется, придираться к чему-либо в богословии».
Невозможно, пишет Беркли, представить себе мгновенную скорость, то есть скорость в данное мгновение и в данной точке, ибо понятие движения включает понятия о (конечных ненулевых) пространстве и времени.
Как же с помощью анализа получаются правильные результаты? Беркли пришел к мысли, что это объясняется наличием в аналитических выводах взаимокомпенсации нескольких ошибок, и проиллюстрировал это на примере параболы. Занятно, что некоторые крупные математики (например, Лагранж) согласились с ним.
Сложилась парадоксальная ситуация, когда строгость и плодотворность в математике мешали одна другой. Несмотря на использование незаконных действий с плохо определёнными понятиями, число прямых ошибок было на удивление малым — выручала интуиция. И всё же весь XVIII век математический анализ бурно развивался, не имея по существу никакого обоснования. Эффективность его была поразительна и говорила сама за себя, но смысл дифференциала по-прежнему был неясен. Особенно часто путали бесконечно малое приращение функции и его линейную часть.
В течение всего XVIII века предпринимались грандиозные усилия для исправления положения, причём в них участвовали лучшие математики столетия, однако убедительно построить фундамент анализа удалось только Коши в начале XIX века. Он строго определил базовые понятия — предел, сходимость, непрерывность, дифференциал и др., после чего актуальные бесконечно малые исчезли из науки. Некоторые оставшиеся тонкости разъяснил позднее Вейерштрасс.
Как иронию судьбы можно рассматривать появление в середине XX века нестандартного анализа, который доказал, что первоначальная точка зрения — актуальные бесконечно малые — также непротиворечива и могла бы быть положена в основу анализа.
О клинических исследованиях
Что такое клинические исследования и зачем они нужны? Это исследования, в которых принимают участие люди (добровольцы) и в ходе которых учёные выясняют, является ли новый препарат, способ лечения или медицинский прибор более эффективным и безопасным для здоровья человека, чем уже существующие.
Главная цель клинического исследования — найти лучший способ профилактики, диагностики и лечения того или иного заболевания. Проводить клинические исследования необходимо, чтобы развивать медицину, повышать качество жизни людей и чтобы новое лечение стало доступным для каждого человека.
Как их проводят?
У каждого исследования бывает четыре этапа (фазы):
I фаза — исследователи впервые тестируют препарат или метод лечения с участием небольшой группы людей (20—80 человек). Цель этого этапа — узнать, насколько препарат или способ лечения безопасен, и выявить побочные эффекты. На этом этапе могут участвуют как здоровые люди, так и люди с подходящим заболеванием. Чтобы приступить к I фазе клинического исследования, учёные несколько лет проводили сотни других тестов, в том числе на безопасность, с участием лабораторных животных, чей обмен веществ максимально приближен к человеческому;
II фаза — исследователи назначают препарат или метод лечения большей группе людей (100—300 человек), чтобы определить его эффективность и продолжать изучать безопасность. На этом этапе участвуют люди с подходящим заболеванием;
III фаза — исследователи предоставляют препарат или метод лечения значительным группам людей (1000—3000 человек), чтобы подтвердить его эффективность, сравнить с золотым стандартом (или плацебо) и собрать дополнительную информацию, которая позволит его безопасно использовать. Иногда на этом этапе выявляют другие, редко возникающие побочные эффекты. Здесь также участвуют люди с подходящим заболеванием. Если III фаза проходит успешно, препарат регистрируют в Минздраве и врачи получают возможность назначать его;
IV фаза — исследователи продолжают отслеживать информацию о безопасности, эффективности, побочных эффектах и оптимальном использовании препарата после того, как его зарегистрировали и он стал доступен всем пациентам.
Считается, что наиболее точные результаты дает метод исследования, когда ни врач, ни участник не знают, какой препарат — новый или существующий — принимает пациент. Такое исследование называют «двойным слепым». Так делают, чтобы врачи интуитивно не влияли на распределение пациентов. Если о препарате не знает только участник, исследование называется «простым слепым».
Чтобы провести клиническое исследование (особенно это касается «слепого» исследования), врачи могут использовать такой приём, как рандомизация — случайное распределение участников исследования по группам (новый препарат и существующий или плацебо). Такой метод необходим, что минимизировать субъективность при распределении пациентов. Поэтому обычно эту процедуру проводят с помощью специальной компьютерной программы.
Преимущества и риски для участников. Плюсы
- бесплатный доступ к новым методам лечения прежде, чем они начнут широко применяться;
- качественный уход, который, как правило, значительно превосходит тот, что доступен в рутинной практике;
- участие в развитии медицины и поиске новых эффективных методов лечения, что может оказаться полезным не только для вас, но и для других пациентов, среди которых могут оказаться члены семьи;
- иногда врачи продолжают наблюдать и оказывать помощь и после окончания исследования.
При этом, принимая решение об участии в клиническом исследования, нужно понимать, что:
- новый препарат или метод лечения не всегда лучше, чем уже существующий;
- даже если новый препарат или метод лечения эффективен для других участников, он может не подойти лично вам;
- новый препарат или метод лечения может иметь неожиданные побочные эффекты.
Главные отличия клинических исследований от некоторых других научных методов: добровольность и безопасность. Люди самостоятельно (в отличие от кроликов) решают вопрос об участии. Каждый потенциальный участник узнаёт о процессе клинического исследования во всех подробностях из информационного листка — документа, который описывает задачи, методологию, процедуры и другие детали исследования. Более того, в любой момент можно отказаться от участия в исследовании, вне зависимости от причин.
Обычно участники клинических исследований защищены лучше, чем обычные пациенты. Побочные эффекты могут проявиться и во время исследования, и во время стандартного лечения. Но в первом случае человек получает дополнительную страховку и, как правило, более качественные процедуры, чем в обычной практике.
Клинические исследования — это далеко не первые тестирования нового препарата или метода лечения. Перед ними идёт этап серьёзных доклинических, лабораторных испытаний. Средства, которые успешно его прошли, то есть показали высокую эффективность и безопасность, идут дальше — на проверку к людям. Но и это не всё.
Сначала компания должна пройти этическую экспертизу и получить разрешение Минздрава РФ на проведение клинических исследований. Комитет по этике — куда входят независимые эксперты — проверяет, соответствует ли протокол исследования этическим нормам, выясняет, достаточно ли защищены участники исследования, оценивает квалификацию врачей, которые будут его проводить. Во время самого исследования состояние здоровья пациентов тщательно контролируют врачи, и если оно ухудшится, человек прекратит своё участие, и ему окажут медицинскую помощь. Несмотря на важность исследований для развития медицины и поиска эффективных средств для лечения заболеваний, для врачей и организаторов состояние и безопасность пациентов — самое важное.
Потому что проверить его эффективность и безопасность по-другому, увы, нельзя. Моделирование и исследования на животных не дают полную информацию: например, препарат может влиять на животное и человека по-разному. Все использующиеся научные методы, доклинические испытания и клинические исследования направлены на то, чтобы выявить самый эффективный и самый безопасный препарат или метод. И почти все лекарства, которыми люди пользуются, особенно в течение последних 20 лет, прошли точно такие же клинические исследования.
Если человек страдает серьёзным, например, онкологическим, заболеванием, он может попасть в группу плацебо только если на момент исследования нет других, уже доказавших свою эффективность препаратов или методов лечения. При этом нет уверенности в том, что новый препарат окажется лучше и безопаснее плацебо.
Согласно Хельсинской декларации, организаторы исследований должны предпринять максимум усилий, чтобы избежать использования плацебо. Несмотря на то что сравнение нового препарата с плацебо считается одним из самых действенных и самых быстрых способов доказать эффективность первого, учёные прибегают к плацебо только в двух случаях, когда: нет другого стандартного препарата или метода лечения с уже доказанной эффективностью; есть научно обоснованные причины применения плацебо. При этом здоровье человека в обеих ситуациях не должно подвергаться риску. И перед стартом клинического исследования каждого участника проинформируют об использовании плацебо.
Обычно оплачивают участие в I фазе исследований — и только здоровым людям. Очевидно, что они не заинтересованы в новом препарате с точки зрения улучшения своего здоровья, поэтому деньги становятся для них неплохой мотивацией. Участие во II и III фазах клинического исследования не оплачивают — так делают, чтобы в этом случае деньги как раз не были мотивацией, чтобы человек смог трезво оценить всю возможную пользу и риски, связанные с участием в клиническом исследовании. Но иногда организаторы клинических исследований покрывают расходы на дорогу.
Если вы решили принять участие в исследовании, обсудите это со своим лечащим врачом. Он может рассказать, как правильно выбрать исследование и на что обратить внимание, или даже подскажет конкретное исследование.
Клинические исследования, одобренные на проведение, можно найти в реестре Минздрава РФ и на международном информационном ресурсе www.clinicaltrials.gov.
Обращайте внимание на международные многоцентровые исследования — это исследования, в ходе которых препарат тестируют не только в России, но и в других странах. Они проводятся в соответствии с международными стандартами и единым для всех протоколом.
После того как вы нашли подходящее клиническое исследование и связались с его организатором, прочитайте информационный листок и не стесняйтесь задавать вопросы. Например, вы можете спросить, какая цель у исследования, кто является спонсором исследования, какие лекарства или приборы будут задействованы, являются ли какие-либо процедуры болезненными, какие есть возможные риски и побочные эффекты, как это испытание повлияет на вашу повседневную жизнь, как долго будет длиться исследование, кто будет следить за вашим состоянием. По ходу общения вы поймёте, сможете ли довериться этим людям.
Если остались вопросы — спрашивайте в комментариях.
Источники:
http://studopedia.ru/4_160667_beskonechno-malie-i-beskonechno-bolshie-funktsii-sravnenie-beskonechno-malih-funktsiy.html
http://dic.academic.ru/dic.nsf/ruwiki/362918
http://yandex.ru/health/turbo/articles?id=2463











.jpg.64ef124648d9bb326a2737bee637a793.jpg)